Field Theory - Online Tutorial 1

by Kevin Tang , last update: Feb 23, 2014, 7.20PM (last one before midterm)

[main pages]

These are some important questions I think will be helpful; you can relax and read them, it can help at some level,

but what most important among all, is you must do the question by yourself at least all the homework questions and all the examples professor show in the class.

* Please think about the solution by yourself too, in case if I made any typo or mistake.

* Notice, all the bold font on this page, means that variable is a vector, for example... E

[Q1 - Electric Field Intensity Question] [ Q2 - Flux Density Question] [ Q3 -  E = − ∇V Question ] [Q4  - Dielectric] [Reminder]

Q1 -

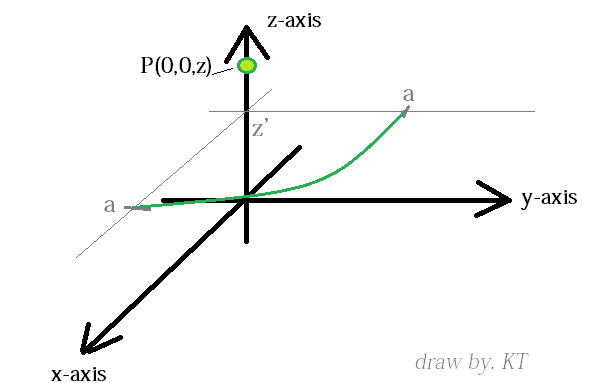
a) Find E at P(0,0,z), given a quarter circle of line charge density ρ_L along the line (the green line) shown in Figure 1.

b) Solve for the same question, where line charge forms a complete circle (i.e. φ : 0 -> 2π)

suggest solving time : 25 min

                                                 Figure . 1

SOLUTIONS 1a) (notice, my solutions is relative longer than what you need to wrote, you do not need to follow some non necessary steps)

To solve this question; first we need  to processed the 5- main steps .. they are following...

Step 1 : Find r

Notice, r is where our reference point at, that is the Green Point on the z-axis

Cartesian Coordinates, we can write P as (0, 0, z) ,...

r = 0a_x + 0a_y + za_z

Step 2 : Find r'

Any point along that green quarter circle line in cylindrical coordinates can write as (ρ , φ, z),

ρ: where you given the constant radius as ρ = a

z: where you given the constant high z as z = z'

φ: where your only changing (non-constant) variable is φ

since in Step 1, we are already in "Cartesian Coordinates", we need to change r' into the same coordinates system - Cylindrical Coordinates,

in your formula sheet, you should able to find the equation on pages 3,...

which shows ρ a_ρ = ρ cos φ a_x + ρ sin φ a_y

a_x part is ... ρ cos φ a_x -->  sub ρ = a in  --- > a cos φ a_x

a_y  part is ... ρ cos φ a_y --> sub ρ = a in  --- > a sin φ a_y

a_z part is ...  z a_z --> z'az a_z

r' =  a cos φ a_x +  a sin φ a_y + z' a_z

Step 3 : Find R = r − r'

r − r' =  ( 0a_x + 0a_y + za_z ) − ( a cos φ a_x +  a sin φ a_y + z' a_z )

         = − a cos φ a_x − a sin φ a_y + (z − z') a_z

Step 4 : Find |R| = |r − r'|

|r − r'| = √ {  (− a cos φ)² + (− a sin φ )² + (z − z')² }

           = √ { a² cos²φ + a² sin² φ +  (z − z')²  }

           = √ { a² ( cos²φ + sin² φ ) + (z − z')²   }   ... where , sin² φ  + cos²φ = 1

           =  √ { a²  + (z − z')² }

and you can check your result directly by visual

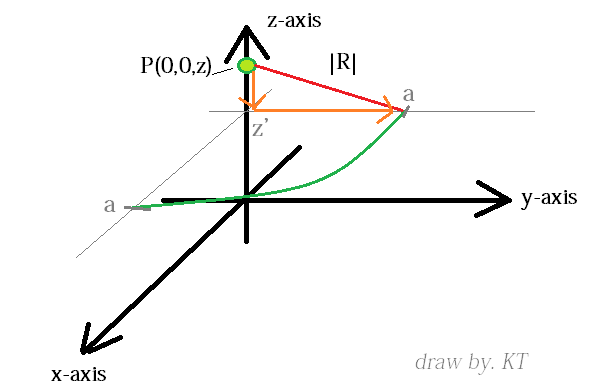
based on pythagorean theorem.; the red line will have the distance ...

|r − r'| = √ { a²  + (z − z')² }

Step 5: Find dQ

What is the change of the enclosed charge along the line, its same as the line charge destiny,

which is ρ_L, therefore, the dQ will be...

dQ = ρ_L dL

where L = ρ * φ   ... the length of circlur line is same as the radius times the angle.

        dL = ρ dφ     ... ρ stay constant and equal to a

        dL = a dφ     .... now you can plug dL it back to dQ

dQ = ρ_L a dφ

Last Steps - Find the E

Now we have following...

(1) ... r = 0a_x + 0a_y + za_z

(2) ...  r' =  a cos φ a_x +  a sin φ a_y + z' a_z

(3) ... r − r' =  − a cos φ a_x − a sin φ a_y + (z − z') a_z

(4) ... |r − r'| = √ { a²  + (z − z')² }

(5) ... dQ = ρ_L a dφ

Put them into the Electric Field intensity (E) equation for line...

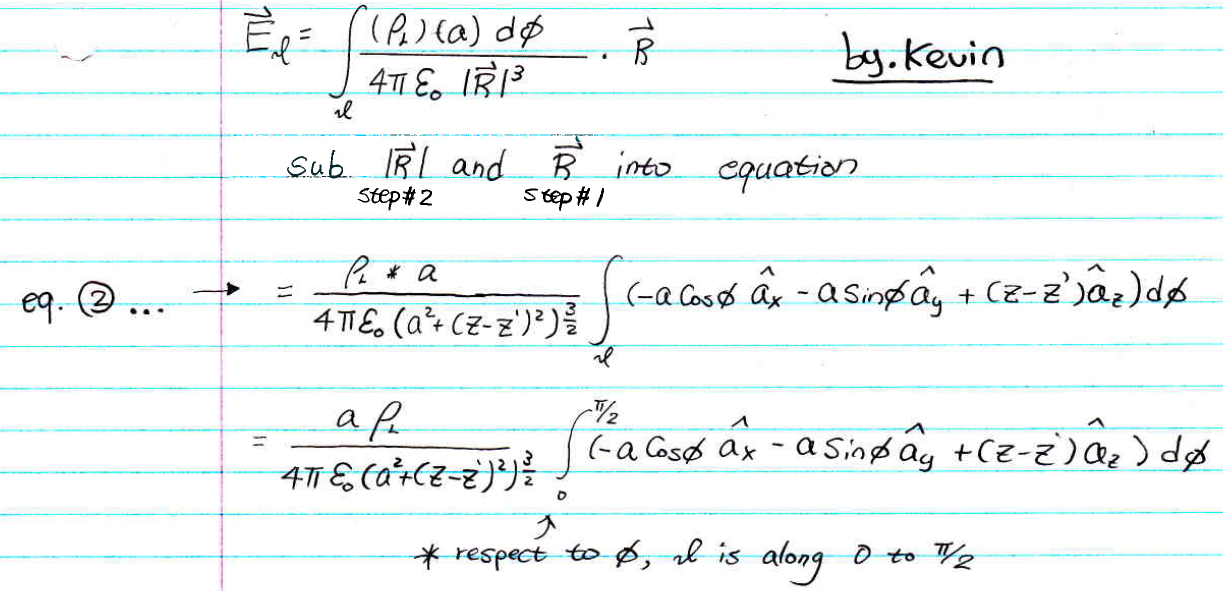
* Remember to write the unit in your final answer, the unit for E is either V/m or N/C

Q1 - b)

Solve for the same question, where line charge forms a complete circle (i.e. φ : 0 -> 2π)

SOLUTIONS 1b)

First of all, you should able to visually see the Line of that quarter circle is now forming a full circle (as I shown in Figure 2)

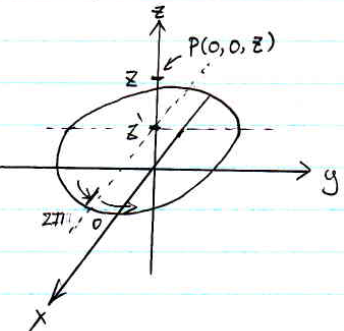
               Figure 2

Noting really change, therefore, you can continue from the last steps from 1a), which we still have the following..

(1) ... r = 0a_x + 0a_y + za_z

(2) ...  r' =  a cos φ a_x +  a sin φ a_y + z' a_z

(3) ... r − r' =  − a cos φ a_x − a sin φ a_y + (z − z') a_z

(4) ... |r − r'| = √ { a²  + (z − z')² }

(5) ... dQ = ρ_L a dφ

However, the integral boundary is changing on the φ part, instead of 0 to π/2 its now 0 to 2π.

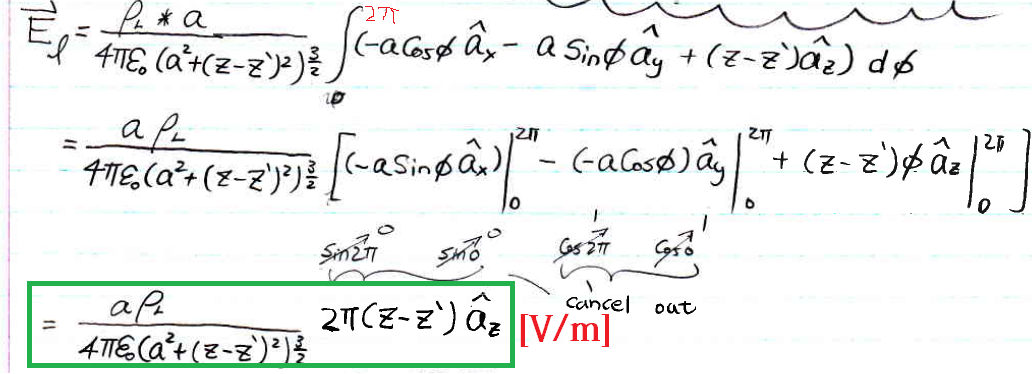
Note for 1b)

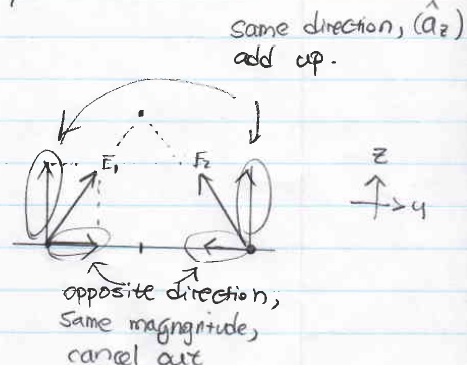
As you can double check your final answer's vector part, you can see there is only part a_z left,

if think visually as all the symmetric vector of Electric Field on the same plane cancel out, left only the vertical direction upward .. a_z

[back to top]

=======================================================================================================

Q2 .

Given a sphere with a hollow sphere inside and located at the centred at the origin, as shown in Figure 3

The hollow sphere part has a radius of "a", and the bigger sphere have the radius of "b"

if we notice the material part have the volume charge density ρ_v = αr [c/m³]

a) Find total charge contained in the sphere.

b) Using Gauss' law and symmetry solve for the electric flux density vector field D in the following regions

i - r <a

ii - a < r < b

iii - r > b

suggest solving time: 30 min

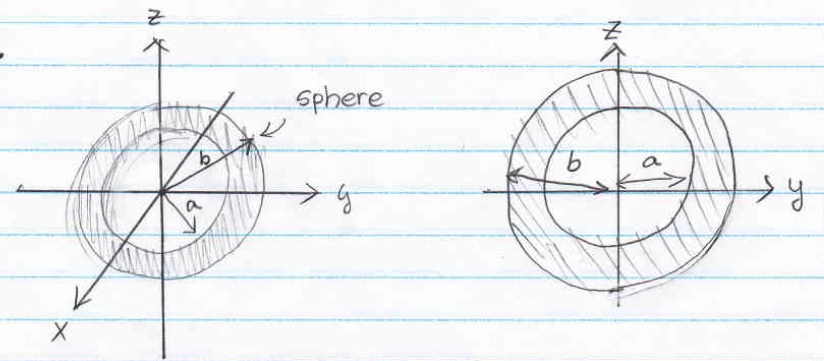
                                                         Figure . 3

SOLUTION 2a)

Its similar, you can see the relationship between Charge and Charge Density as following...

Q_v =  ∫_v ρ_v dv   ... (volume)

Q_s = ∫_s ρ_s ds   ... (surface)

Q_l = ∫_l ρ_l dl   ... (line)

Select the volume one,

Q_enc =  ∫_v ρ_v dv       

         = ∫∫∫ αr * r² sin θ dr dθ dφ                       <---- notice, dv = r² sin θ dr dθ dφ  in sphere coordinate.

         = ∫_r=a ^b ∫_θ=0^π ∫_φ=0^2π  αr³ sin θ dr dθ dφ   <---- notice, as said in class, the boundary of θ cannot go over π.

                                                                                and the boundary for "r" is between a and b, b/c that is where the charge is located.

         = α ∫_r=a ^b ∫_θ=0^π ∫_φ=0^2π r³ sin θ dr dφ dθ   < --- α is a constant, you can pulled it to the front of the integral

         = α ∫_r=a ^b r³ dr   ∫_θ=0^π sin θ dθ ∫_φ=0^2π dφ  

         = α [(1/4)r⁴ |_r=a ^b][− cosθ |_θ=0^π][φ |_φ=0^2π ]

         =  α [(1/4)(b⁴ − a⁴)][− cosπ + cos0][ 2π − 0]

         =  α [(1/4)(b⁴ − a⁴)][2][2π]

         = απ  (b⁴ − a⁴)

Answer : Q_enc= απ  (b⁴ − a⁴)  [C]

SOLUTION 2b)

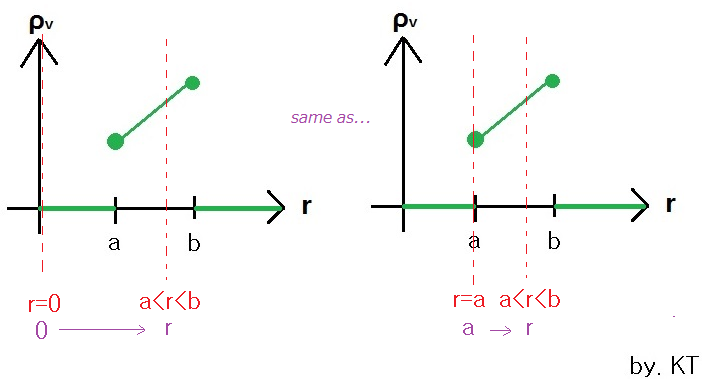
First, before you start, take a look at the volume charge density, which is ρ_v = αr

and this equation only applied between charged region (which is between r= a to r = b),

therefore, I can draw a equation of ρ_v = αr as following...

(notice, you don't have to do this on the exam).

Start with finding the enclosed charge Q_enc that respect to each assigned region

i - for r < a

Similar as what we did in 2a), but the different is that this time,

the r is bounding between r= 0 to r, where r is less than a,

notice, if we are at r<a, this region, the ρ_v = 0, therefore, you just simply plug ρ_v = 0 replace with ρ_v

by doing so,.. you end up with D = 0 [c/m²], as shown following

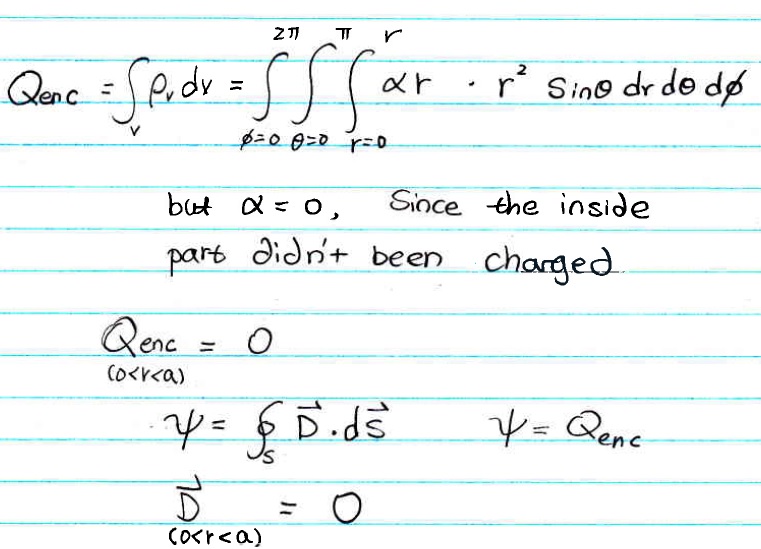
ii - for  a < r < b

The boundary for r is the same as from 0 to r, where r is between a and b.

The lower boundary will be a. (as shown in diagram, the lower boundary of r become "a" instead "0" since from 0 to a there are no charge)

The upper boundary will be r. (as shown in diagram, the upper boundary is r, it is a changing variable)

(common mistake, the upper boundary of "r" is NOT b, notice, r is less than b but greater than a,

  therefore the upper boundary is simply a changing variable, you should write "r" on your upper boundary)

you can than wrote down Q_enc for a<r<b as following.

iii - for  r > b

The boundary for r is the same as from 0 to r, where r is greater than b.

The lower boundary will be a. (as shown in diagram, the lower boundary of r become "a" instead "0" since from 0 to a there are no charge)

The upper boundary will be b. (as shown in diagram, the lower boundary of r become "b" instead "r" since from b to r there are no more charge)

(common mistake, the upper boundary of "r" is NOT r, notice, r is greater than b, and if its greater than b, as you can see in diagram,

  more than b, its already make charge density at full level, the upper boundary is a fixed variable as b)

you can than wrote down Q_enc for r>b as following.

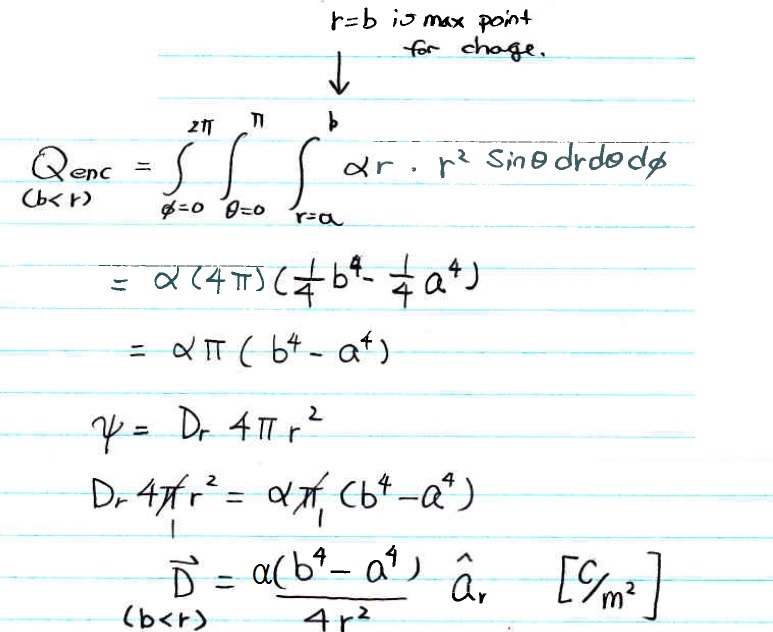
Finally, we got the D for each region as...

[back to top]

=======================================================================================================

Q3.

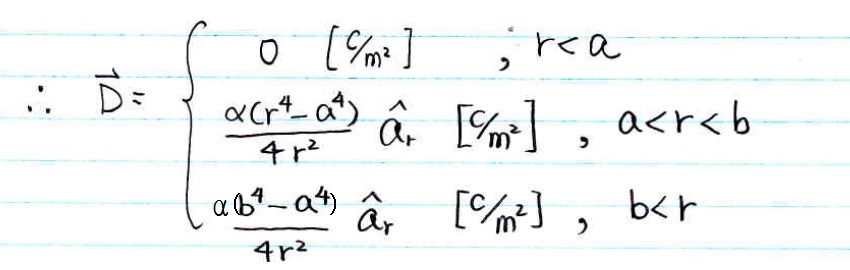
Given V = Sin θ / r, find the following ... 

(notice, this kind question could be V = xyz  or V = ρ Cos φ ...etc ,

 which are the same type question, just use different coordinate system)

a) E

b) D

c) ρ_v

d) Q_enc with in a sphere which 0<r<1, 0<φ<90^o, 0<θ<180^o

suggest solving time : 15 min

SOLUTION 3)

First, you need to check which coordinate system does it belong to...

in case we have θ and r, you notice we are in "Sphere Coordinate"

a) First, write down this relationship...

E = − ∇V

we got,.. ∇V = ∂/∂r V a_r  + (1/r) ∂/∂θ V a_θ + (1/r sinθ) ∂/∂φ V a_φ  ... you can solved for E...

b) D = ‎ε_oE

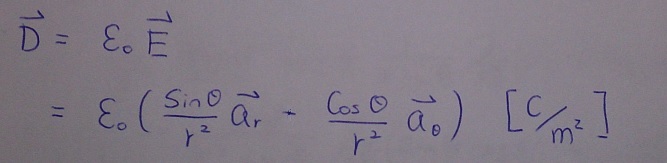
c) ρ_v = ‎∇·D

         = (1/r²) ∂/∂r (r² D_r) + (1/r sinθ)∂/∂θ (sinθ D_θ)  + (1/r sinθ) ∂/∂φ D_φ

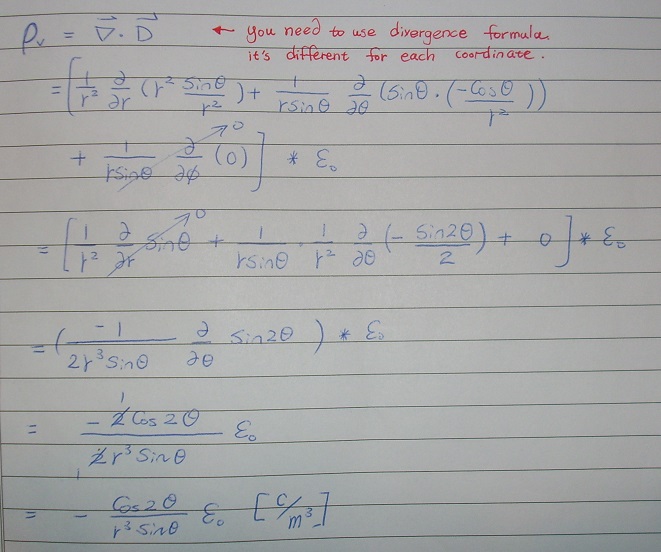
d) Q_enc =  ∫_v ρ_v dv

              = ∫_r=0 ¹ ∫_θ=0^π ∫_φ=0^2π  ρ_v r² sin θ dr dφ dθ

[back to top]

=======================================================================================================

Q4.

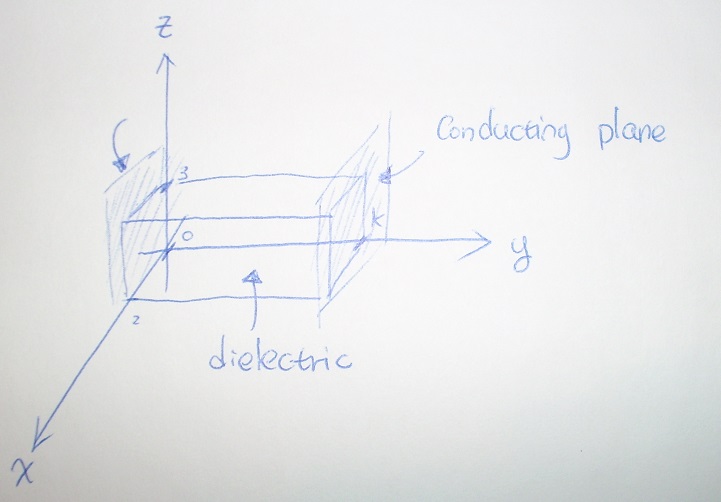
A dielectric material box, have the following size, 0 < x < 2, 0 < y < k, 0 < z < 3,

the box is been placed between two conducting planes located at y = 0 and y = k. 

If the polarization vector field inside the dielectric  material is

                   P = (ny³ + m) a_y [c/m²]

find the following...

a) E

b) D

c) ρ_s at y = 0^-

d) ρ_s at y = k⁺

e) ρ_v

f) ρ_ps at y = 0⁺

g) ρ_ps at y = k^-

h) ρ_pv

SOLUTION 4)

First, some student told me they didn't know dielectric is covered for the midterm,

which it is covered, so please read them, at last tutorial, we covered this question, so please review it too :)

To start with the question (I changed it),

you can draw that box out, which should be easy for you.

a) There are relationship between P and E, please review Chapter 5.

You need to use the following relation

P = X_eε_oE

where X_e = ε_r− 1

b)

c)

d) Same as in c

however, this time your a_n become −a_y

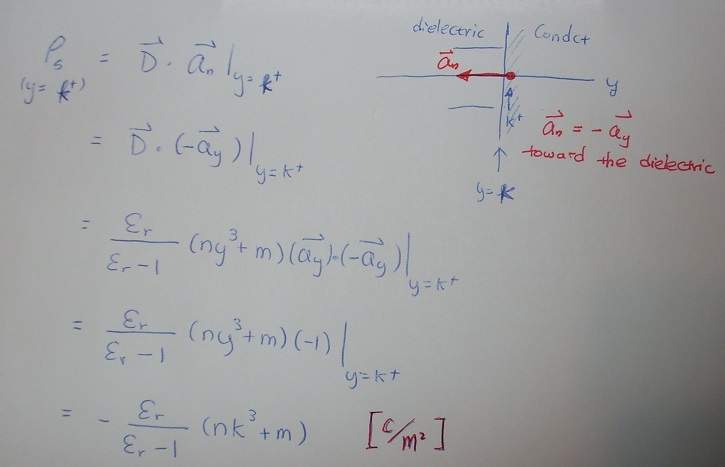
e) ρ_v = ‎∇·D

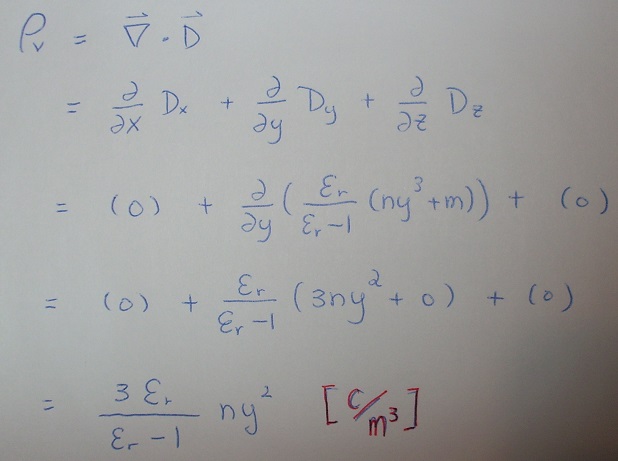
f) ρ_ps  is called polarization surface charge density, similar as what you did above

just you are looking at dielectric part instead of condt part, at y = 0+

g) ρ_ps  at y = k-

h) Very similar as you find in part e), the equation for

    polarization volume charge density is ρ_pv =  − ‎∇·P

[back to top]

=======================================================================================================

Reminder

Sine some people asked, remind you,

here is how represent a point in vector form in all three coordinate

example points --->

(1, 2, 3) -->  a_x + 2a_y + 3a_z

(2, 90^o, 3) --- > 2a_ρ +  3a_z

(3, 90^o, 195^o) ----> 3a_r

Don't forget few things..

Don't forget to label your x-axis, y-axis, z-axis

Don't forget the unit in your final answer

Don't forget your vector sign if you are solving for a vector

Don't forget, your formula sheet won't able to help you find all the formula you need (such as ρ_v = ‎∇·D, P = X_eε_oE ,... etc won't be on the formula sheet).

Don't be scared, you all passed MTH312, you can do it.

Don't forget what I said in the tutorial class,... good luck, wish you all the very best :)

[back to top]

You may leave me any message if you have any questions, I will try to answer ASAP, thanks and good luck :)