Field Theory - Online Tutorial 2

by Kevin Tang , last update: Apr 27, 2014, 2:00PM

[main pages]

ELE401 Final Exam Review Notes (My own note, it have some important formulas that you should know for your final exam) [3.65MB] .. [ Download Here ]

A Letter From Kevin :D

Q1 -

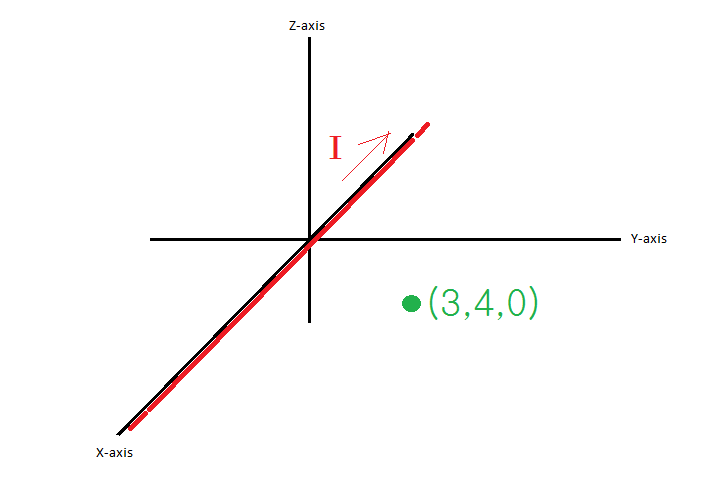
A infinite filaments is placed on x-axis.  (as shown in Figure #1).  It carries current I = 2[A] in negative x-direction.

a) Find the magnetic field intensity vector a_Φ at (3, 4, 0).

                                           Figure #1

Choice one of the following answer.  (Solving Time: 1 min)

SOLUTION 1a)

How to find it?

Simply perform the cross product between the current direction and direct direction.

That is −a_x (current direction a_l) × a_y (from the line to the point direction a_ρ) is equal to −a_z

a_Φ = a_l × a_ρ

      both a_l and a_ρ are in UNIT VECTOR

−a_{z =} −a_x  × a_y   

Another way you can find direction as following...

First, put your RIGHT HAND (in case if you don't know which hand is right hand, its the opposite side to your heart *for most people) on

the CURRENT LINE, point your RIGHT HAND THUMB at same direction as the CURRENT GOES

(shown in Figure #2)

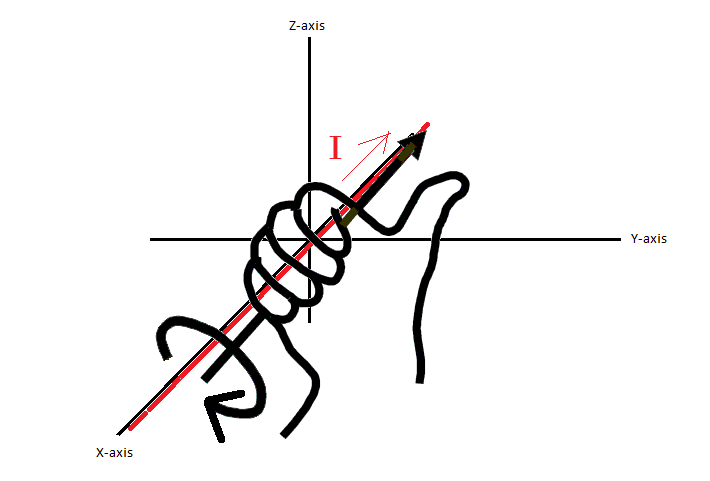
                               Figure # 2

Now, ROTATE as your hand goes, this is your FLUX DIRECTON

as you can see, if you looking from positive X direction toward negative X direction, it is CLOCKWISE

when the FLUX hit the our TARGET POINT (3, 4, 0), its PUSH DOWN toward negative Z (−a_z)direction 

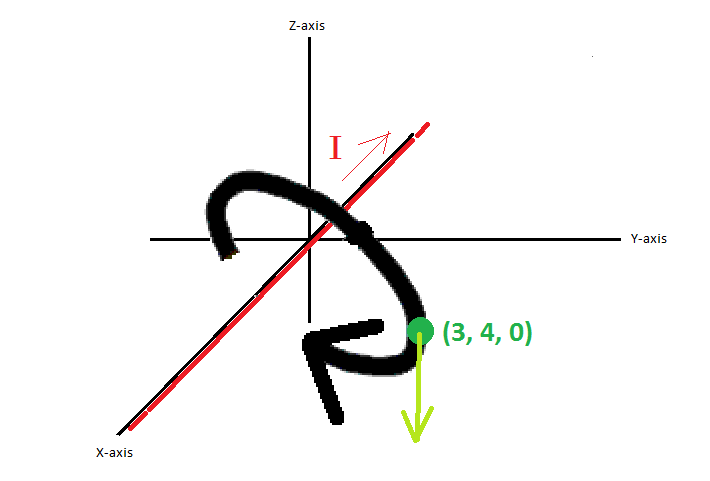
                                         Figure # 3

Looking to the Z-Y Plane, you can see it more clear. (shown in Figure #4)

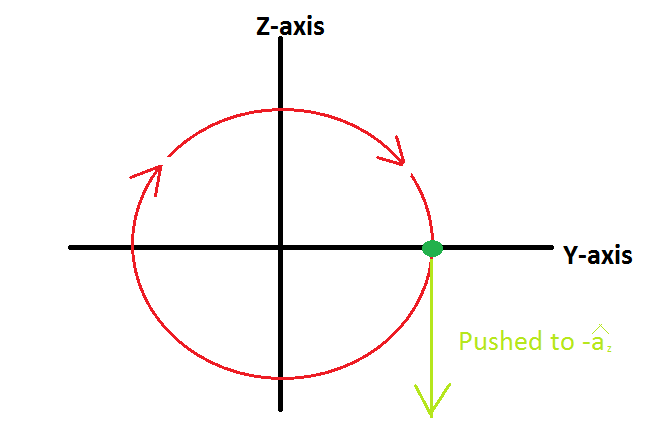
                               Figure # 4

*Important Notice, some case (most case), don't forget the step for unit vector,

  our case it cancel out, because √ (3²+ 0²) = 3 , where 3/3 = 1.

1b)  Now, find H at (3, 4, 0), same graph

Maximum Solving Time : 3 min

SOLUTION 1b)

What is the equation for the line current affect on a single point?

The following equation you need to know ... (eq.1)

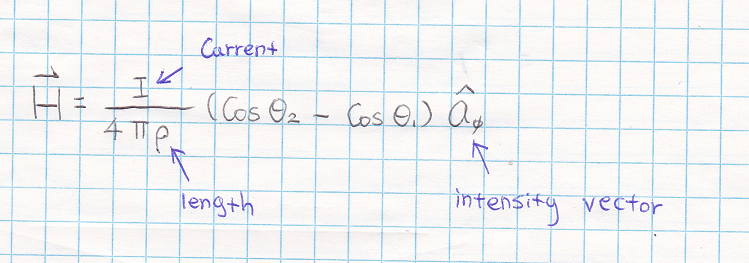  ... eq.1

Where, θ₁ and θ₂ are located as following. (shown in Figure 5)

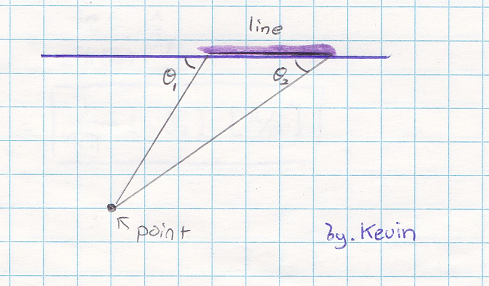
                        Figure #5

Now, when we have an infinite line, where θ₁ will be approach 180^o and  θ₂ will approach 0^o (shown in Figure #6)

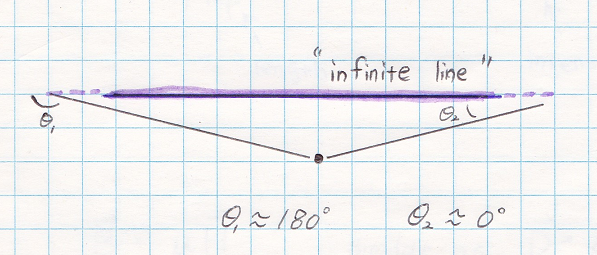
                Figure # 6

Put everything in, you have the equation for Infinite Line (shown in Figure #7)

                               Figure #7

With this, your last step is just put everything in,

notice, your ρ is the shortest distance from your line (extend parallel) to your point.

In our case, its equal to 4 (shown in Figure #8)

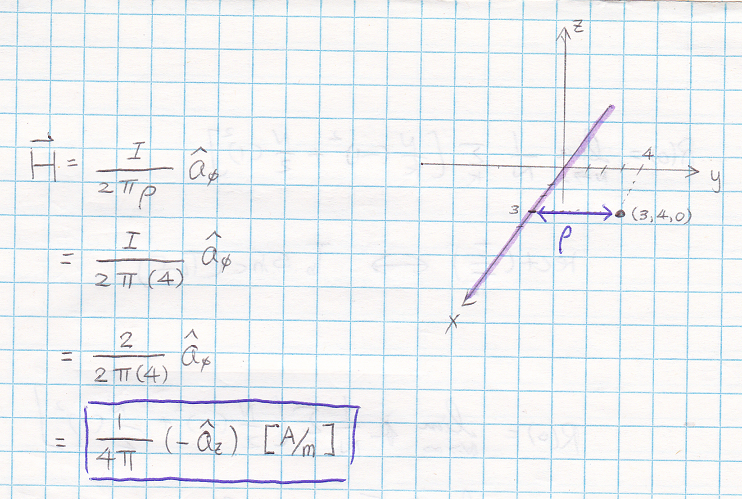
                            Figure #8

Now, you get the final answer -- which is B.

1c) - Given μ = μ_o, please find B at (3, 4, 0), same graph

Maximum solving time: 1 min

This should be very simple, the relation between B and H is as following...

(the way I think, they are brothers or sisters, B is brother for H, as well as D is brother for E)

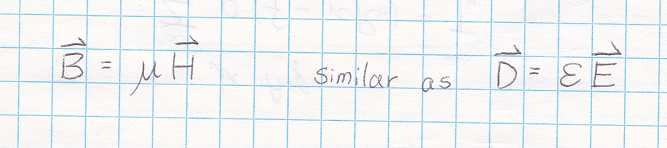
Just multiply it by the constant μ_o,.. than you get your answer..

The only thing some people may forget is the UNIT for the B, its "Tesla" (T)

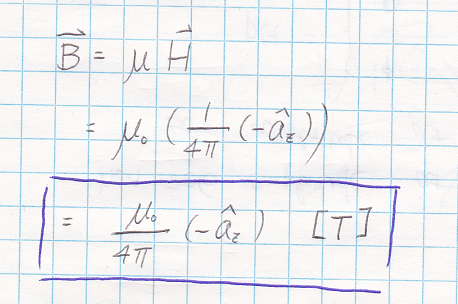
So the answer is D, very easy right? lol

* Note: also, T = Wb/m²

Q2 -

Find the work to move the conductor with current I flow in positive a_z direction,

of the length L₁, the conductor is been placed vertically upward at (c, 0, 0),

for one full revolution about the z-axis if the magnetic flux density B = B₀ρa_ρ.

the revolution shape is a circular shape with radius r = c [m].

.       

SOLUTION 2)

dF = Idl × B

where dl = dza_z

(notice this dl is the conductor line, with length L₁)

Idl × B = I (dza_z × B₀ρa_ρ)

                = I B₀ρa_Φ

notice ... a_z × a_ρ = a_Φ

dF = I B₀ρdz a_Φ

than, take integral on both side...

 F = ∫₀^L I B₀ρdz a_Φ

    = L₁IB₀ρ c a_Φ [N]

After you find the force, than

dW = F · dl

where dl = ρdΦa_Φ

(This dl is respect to the "one full revolution")

dW = (L₁I B₀ρ c a_Φ) · (ρdΦa_Φ)

       = L₁I B₀ c² dΦ  ... where ρ = c

W = ∫₀^2π L₁I B₀ c² dΦ

   = 2π L₁I B₀ c² [J]

ANSWER: W = 2π L₁B₀ρ c² [J]

Q3 - Bio-savart Law question

Base on George's request, this is our question lol

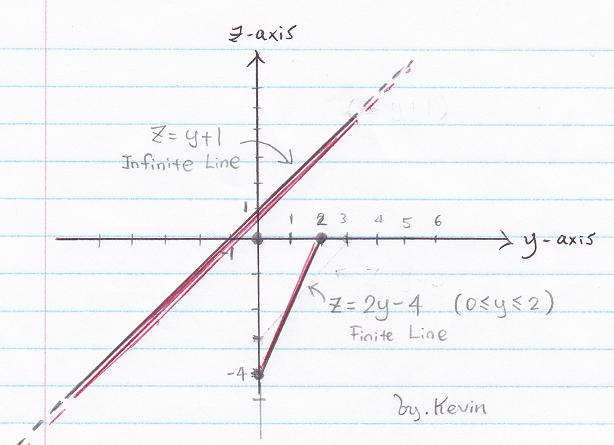
Find H at origin (0, 0, 0), given 2 current line,

Line 1: z = y + 1 (−∞ < y < ∞), current = 2[A] is flowing from negative y direction toward positive y direction.

Line 2 : z = 2y − 4 (0 < y < 2), current = 1[A] is flowing from positive y direction toward negative y direction.

a) Draw the diagram

b) Find H₁

c) Find H₂

d) Find H

SOLUTION Q3)

To find the H, we can split into H = H₁ + H₂ , where H₁ is the H respect to line 1 and H₂ is respect to line 2

First, draw the diagram, you can see the line relationship are all between y and z, so its y-z plan

So, we start with H₁,

looking at line 1 respect to the origin point, use RIGHT HAND RULE, you can see its going toward NEGATIVE X (-a_x) DIRECTION,

well, the only issue is you won't able to find the unit vector using right hand rule (but you can use it to check the answer)

the same thing you can applied using equation a_Φ = a_l × a_ρ

where a_l is the direction of the current flowing

where a_ρ is the direction from the LINE to the TARGET POINT

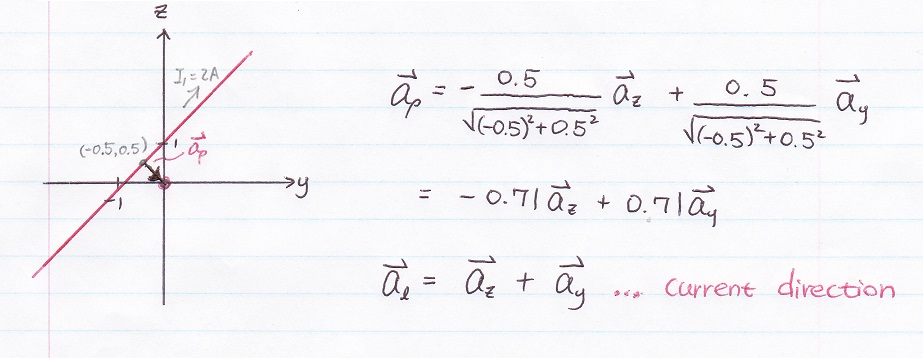
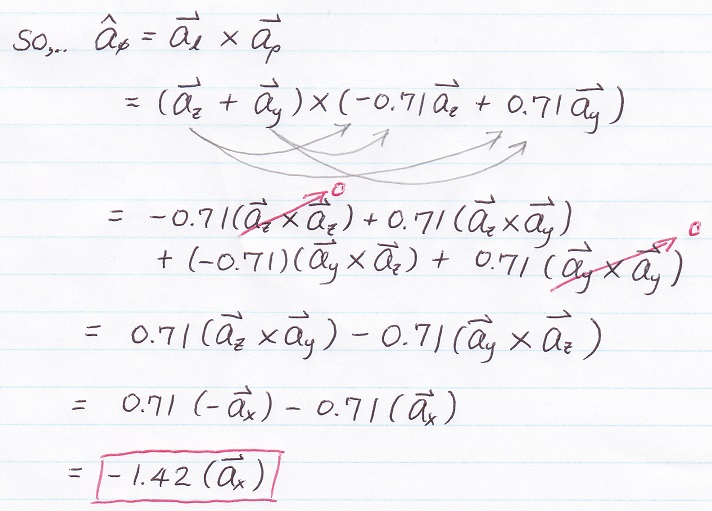
ρ is the shortest distance to the extend line (if line is finite, extend the line all the way, ρ will be the shortest distance of this extend line to the point)

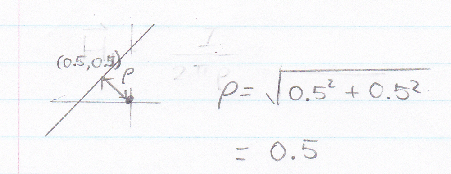
Than, you got your H₁...

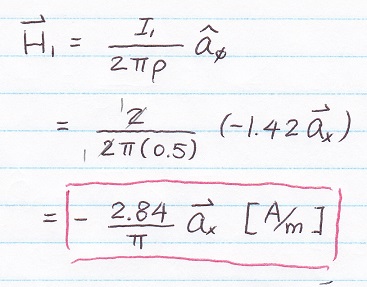
Next, find H2

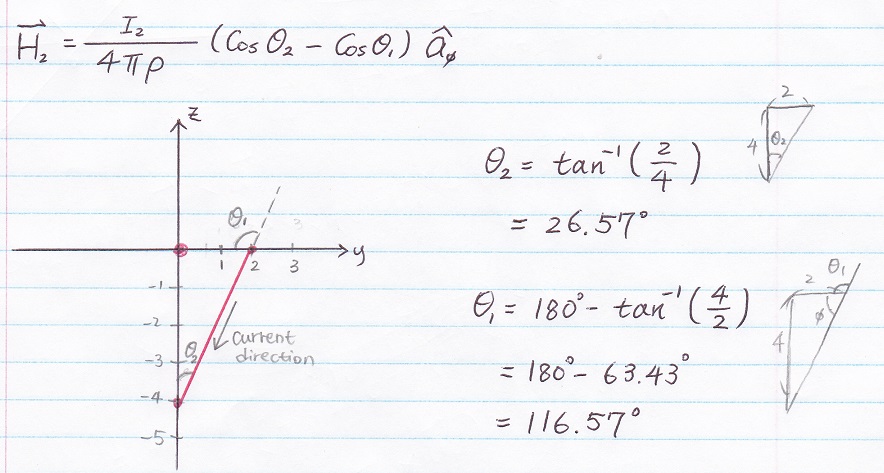
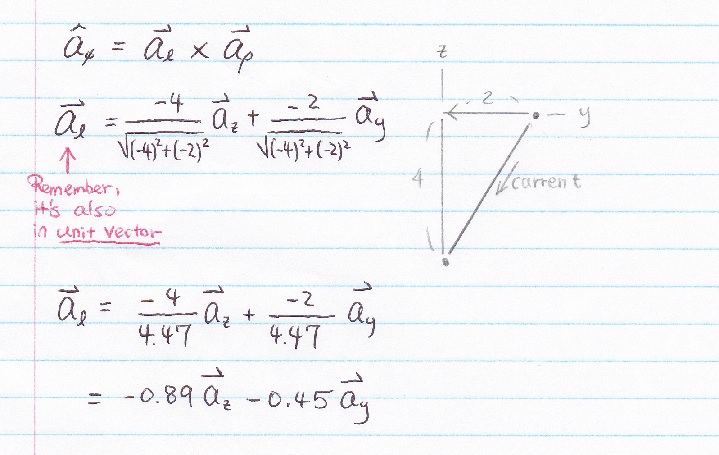
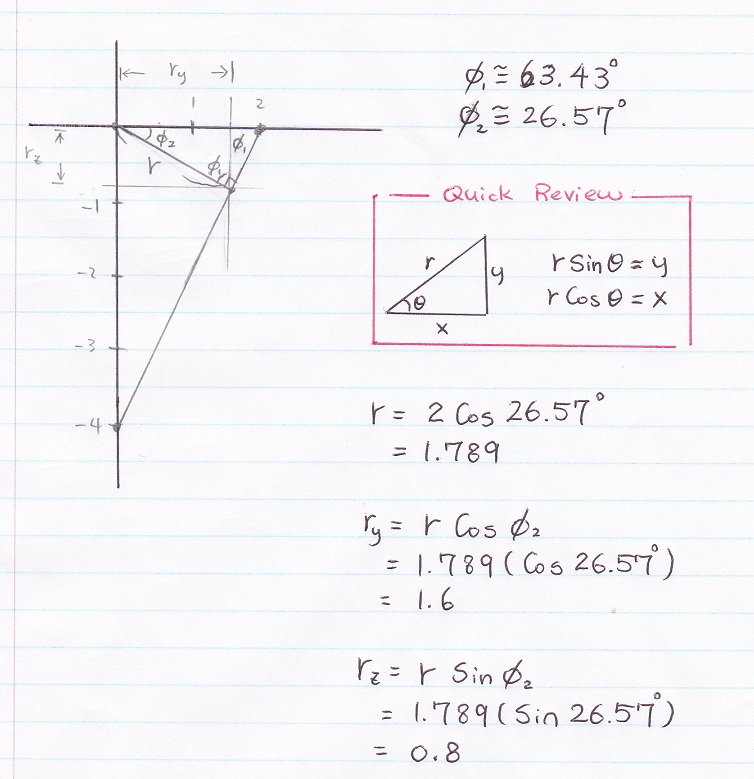
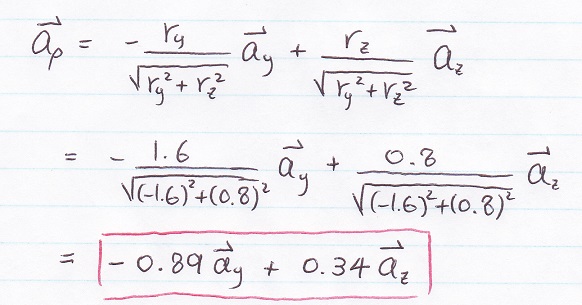
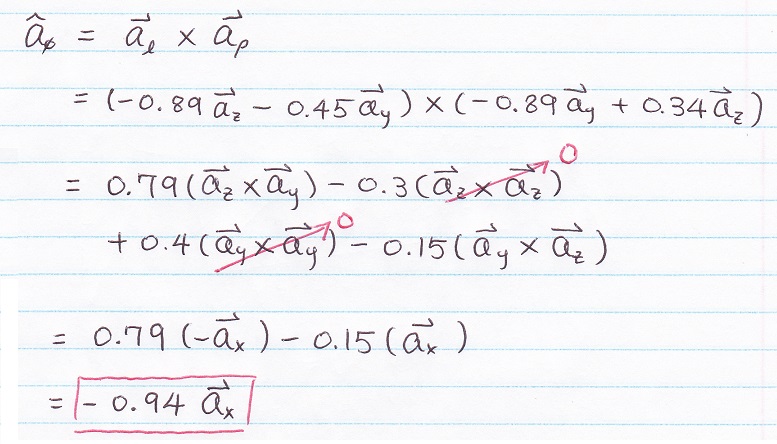
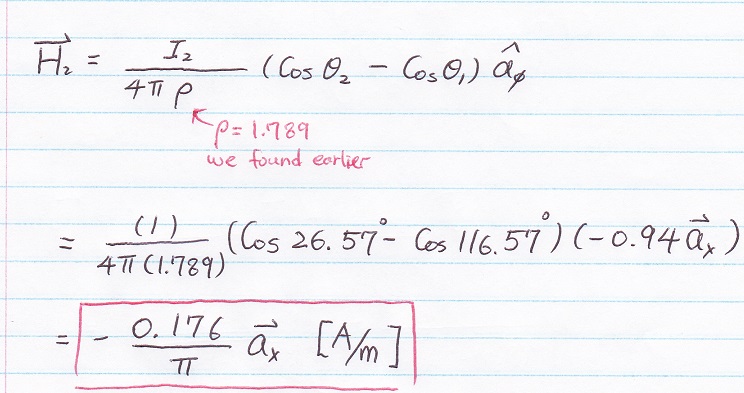
Last step... Just add up H₁ and H₂

H = H₁ + H₂

*Notice, on the exam, it could be a circular current line instead of straight line...

  nothing really change, just use the same concept as you start with

  a_Φ = a_l × a_ρ  the al than will be circular unit vector, the a could be the radius unit vector...

  so you cross it, got the result, ... just think more before you start any question

* Question for F (force) and T (torque)

[back to top]

You may leave me any message if you have any questions, I will try to answer ASAP, thanks and good luck :)