Field Theory - Online Tutorial 3

by Kevin Tang , last update: Jul 1st, 2014

[main pages]

Q1 -

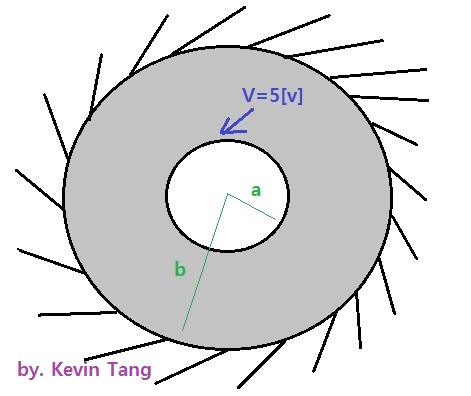
Given a spherical capacitor that have a inner and outer radius a [m] and b [m].

Where voltage will be following... V(r=a) = 5 [V], V(r=b) = 0[V] as shown in Figure #1.  Given ε = ε_o and conductivity constant = σ

Find the following...

1a) Write down Laplace's Equation

1b) V (a < r < b)

1c) E

1d) ρ_sa when r = a

1e) Q when r= a

1f) C at r =a

1g) Energy Density

1h) Total Energy

1i) G conductivity, when r = a, given conductivity constant = σ

                                Figure # 1

1a) Write down Laplace's Equation

Solving Time : 10 sec

If you are not sure which one is Laplace's Equation, please review it right now~

.

.

.

.

.

.

.

SOLUTION 1a)

Yes, very simple ... its ∇²V = 0

Notice, Laplace's equation is from the Poisson's equation, its a "special case" of Poisson equation, where as following...

∇²V = − ρ_v/ ε  .... Poisson's equation

when you are in charge-free region, which ρ_v = 0

so it became.. ∇²V = 0

1b) Find V (a<r<b)

Solving Time: 10 min   ... lets give a try :D

V (a < r < b) = ? which one?

SOLUTION 1b)

Here is how you solve it, please actually go over it at least "once" by yourself.

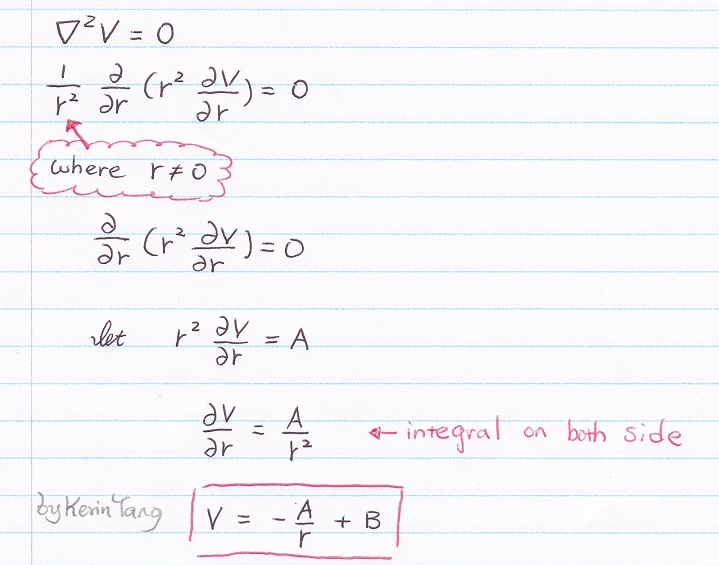
(Please don't forget the condition, that r CANNOT equal to zero)

Next, our target is to find A and B, 2 unknown so you need at least 2 equations,

sub the voltage value, V(r=a) = 5 and V(r= b) = 0 to make 2 equations.

Now, let's find out A = ? and  B = ?

...

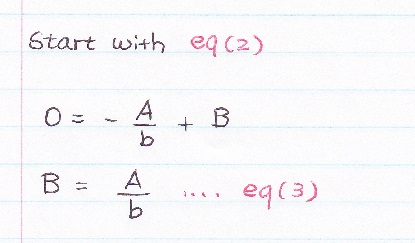
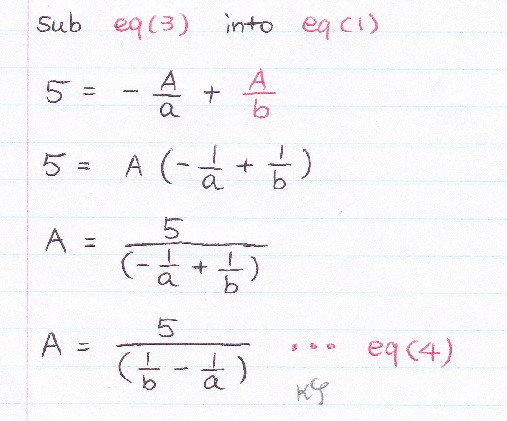
Almost finished...

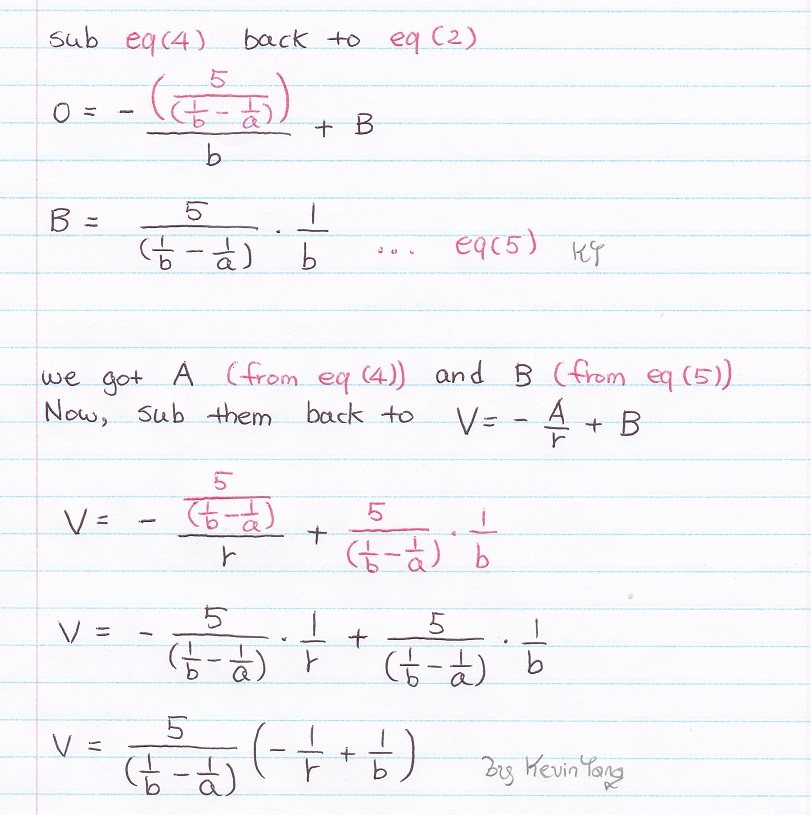
The answer for V(a<r<b)

....

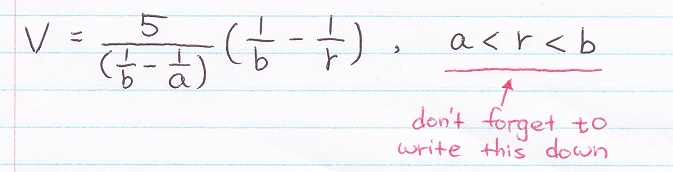
1c) Find E

Maximum solving time: 5 min

SOLUTION 1c)

Simply E = − ∇V

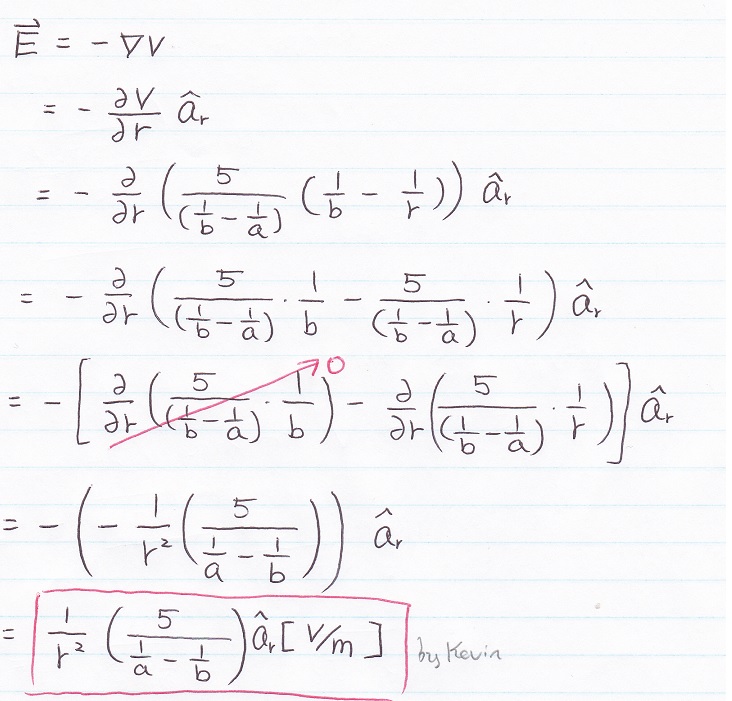
1d) Find ρ_sa at r = a  (where ε = ε_o)

Suggest Solving Time: 5 min

.

.

.

.

.

.

SOLUTION 1d)

* If you choice A ... ρ_sa is a scalar not a vector.

* If you choice B ... don't forget to sub r = a at the end.

* If you choice C ... you are cool :D

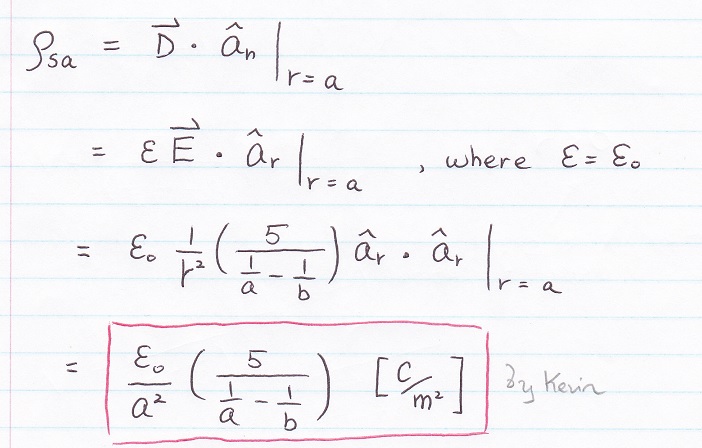
1e) Find Q when r= a

Suggest Solving Time: 2 min

SOLUTION 1e)

1f) Find C when r = a

Suggest Solving Time: 1 min

SOLUTION 1f)

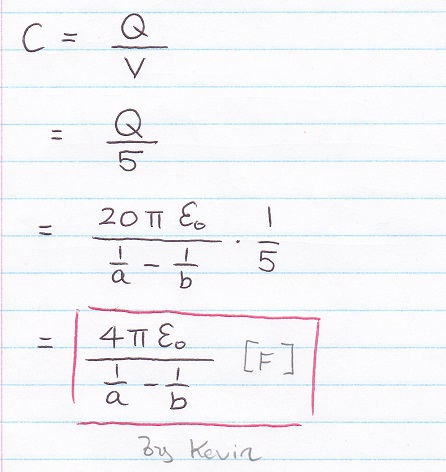
1g) Find Energy Density

Suggest Solving Time: 2 min

SOLUTION 1g)

The symbol of energy density is small case w_e

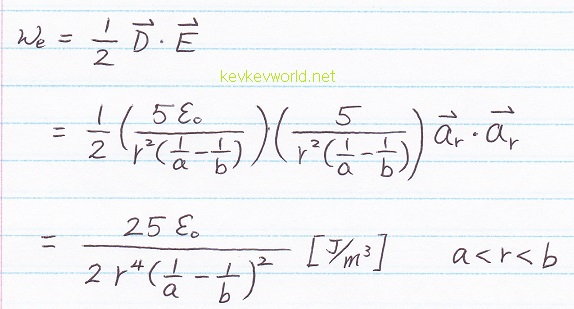
1h) Find Total Energy

Suggest Solving Time: 3 min

SOLUTION 1h)

The symbol of Total Energy is capital case W_e

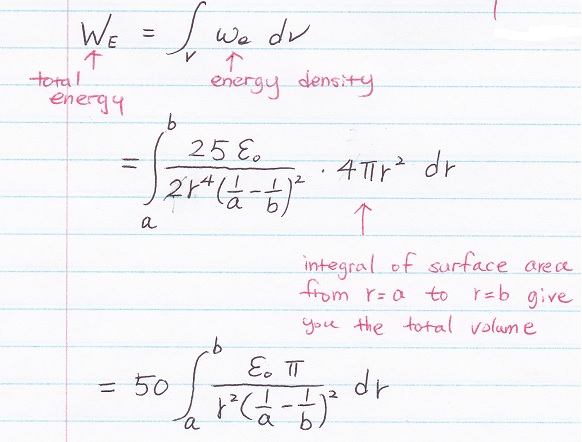
* Note: The integral of surface area respect to the change of radius, can lead you directly to the volume, no need to perform triple integral here.

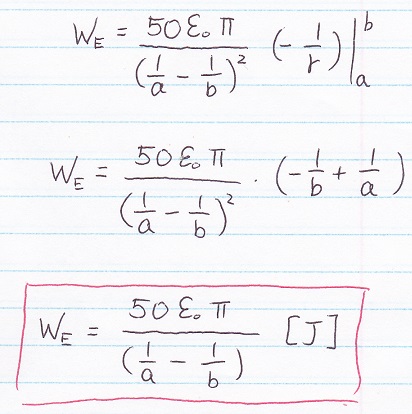
1i) G conductivity, when r = a, given conductivity constant = σ

Suggest Solving Time: 3 min

SOLUTION 1i)

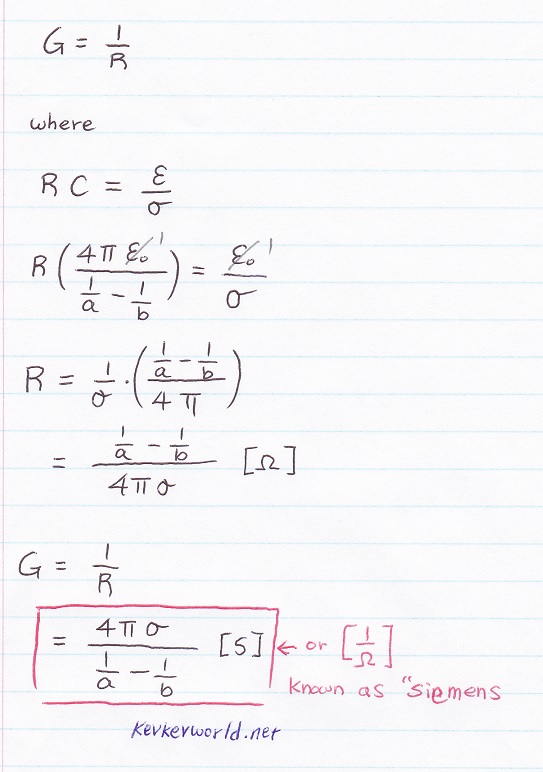
Q2

An infinitely long transmission line consisting of two concentric cylinders having their axes along z-axis.  The inner conductor has radius "a"

and carrying current I, while the outer conductor has inner radius b and thickness t and carries return current - I.

Find the following...

a) Draw the diagram (show the detail label)

b) Find the magnetic field strength H everywhere

c) Find the magnetic flux B everywhere

d) Find the self inductance of inner conductor

SOLUTION a)

If you choice A, you got it wrong, as it said the inner conductor has radius of "a", the current is running inside it, so the i = +I will be inside "a"

If you choice B, you are cool~ :D

b) Find the magnetic field strength H everywhere

SOLUTION b)

First you should able to see there are "4" regions.

Region 1 :  0 < ρ < a

Region 2 :  a < ρ < b

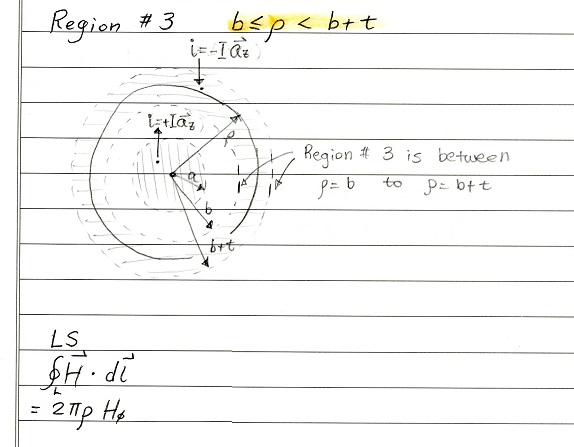
Region 3 :  b < ρ < b + t

Region 4 :  b+ t < ρ

Remember, left side stay the same, only the right hand side is chaging

For Region 1





For Region 2






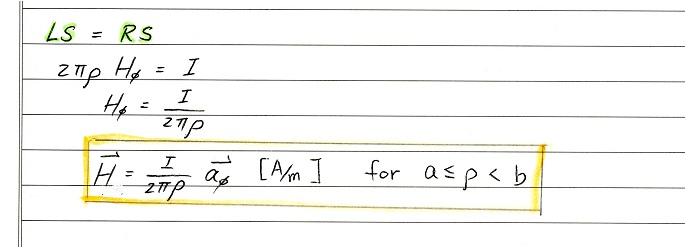
For Region 3
Notice, the LS side is still the same (line integral part)






For Region 4
H = 0 [A/m].... why?

Due to the the total enclosed current equal to zero when you are outside b+t, as I + (-I) = 0

c) Find

d) Self Inductance

Last note:

Good luck, its my very pleasure to work with all of you :)

[back to top]

You may leave me any message if you have any questions, I will try to answer ASAP, thanks and good luck :)