Graphing - Part I

Prepared for Gina. L

Domain and Range

Domain - set of "input (x)" value where function is defined.

Range  - set of "output (y)" value where function is defined.

Question 1.1

Sketch and find the domain / range for following functions.

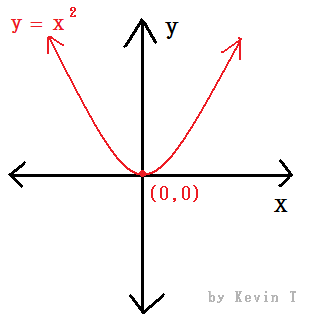
a) y = x² ;  b)  y = √(x + 2)  ; c) y = |x|  ; d) y = 1/x  ;  e) y = sin(x) ;   f) y = log (x + 1)

Solution 1.1

a) y = x²

Domain (-∞, ∞) 

Range [0, ∞)

b) y = √(x + 2)

Domain [-2, ∞)

Range [0, ∞)

c) y = |x|

Domain (-∞, ∞)

Range [0, ∞)

d) y = 1/x

Domain (-∞, 0) ∪  (0, ∞) 

Range (-∞, 0) ∪  (0, ∞)

e) y = sin (x)

Domain (-∞, ∞)

Range [-1, 1]

f) y = log (x + 1)

Domain (-1, ∞)

Range (-∞, ∞)

Even / Odd function

A function can be even, odd or neither.  

If it's an even function, than it have a symmetry relation as...

                         f(x) = f(−x)

If it's an odd function, than it have a symmetry relation as...

                         f(x) = −f(−x)

Otherwise, its neither.

Question 2.1

Determine whether the following function is even, odd or neither.

a) f₁(x) = x²  ;  b) f₂(x) = x³  ;  c) f₃(x) = |x|  ;  d) f₄(x) = √x  ;  e) f₅(x) = x⁴ + 2x³

Solution 2.1

a) f₁(x) = x²

Step 1: Get f₁(−x) 

f₁(−x) = (−x)²

          = x²

Step 2: Compare f(−x) with f(x).

f₁(x) = x² = f₁(−x) 

Step 3: Result

Answer: f₁(x) is an even function.

b) f₂(x) = x³

f₂(−x) = (−x)³

          = −x³

f₂(x) = x³ = −(−x³) = − f₂(−x)

f₂(x) = −f₂(−x)

Answer: f₂(x) is an odd function.

c) f₃(x) = |x|

f₃(−x) = |−x|

          = |x|

f₃(x) = |x| = f₃(−x)

f₃(x) = f₃(−x) 

Answer: f₃(x) is an even function.

d) f₄(x) = √x

f₄(−x) = √(−x)

f₄(x) = √x  ≠ √(−x) = f₄(−x)

f₄(x) = √x  ≠ −√(−x) = −f₄(−x)

Answer: f₄(x) is neither.

e) f₅(x) = x⁴ + 2x³

f₅(−x) = (−x)⁴ + 2(−x)³

          = x⁴ − 2x³

f₅(x) = x⁴ + 2x³  ≠ x⁴ − 2x³ = f₅(−x)

f₅(x) = x⁴ + 2x³  ≠ −x⁴ + 2x³ = −f₅(−x)

Answer: f₅(x) is neither.

... to be continue

Written by Kevin Tang (Mar 9, 2010)

[back]

Copyright 2010 - KEVKEVWORLD.NET