Graphing - Part III

　Prepared for Gina. L

Question 1: Find domain, x-intercept points, y-intercept points, symmetry, all the asymptotes 

and find the actual function base on the given graph (shown on Figure#1).

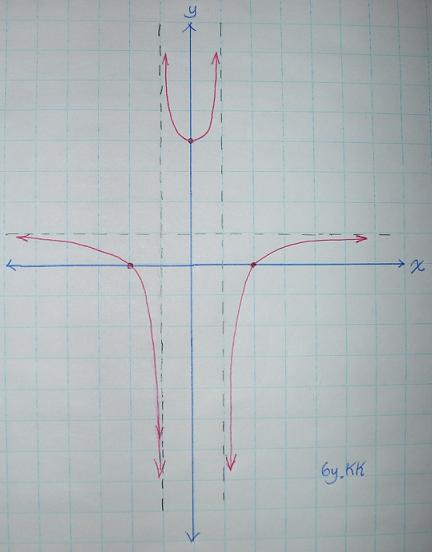
                                      Figure#1

1 - Domain 

Base on Figure#1, we can easily see that there are two vertical asymptotes at x = 1 and x = −1,

therefore,  Domain (−∞, −1)∪(−1, 1)∪(1, ∞)

2 - X- intercepts points

Base on Figure#1, the x-int points are (2, 0) and (−2, 0) 

3 - Y- intercepts points

Base on Figure#1, the y-int point is (0, 4)

4 - Symmetric

There is symmetric about the y-axis, this is an even function, y(x) = y(−x).

5 - Asymptotes

Two vertical asymptotes, x = 1 and x = −1.

One horizontal asymptotes, y = 1.

No slant asymptotes (oblique asymptotes)

6 - Actual Function

6-1

Let y = f(x).

from the x-intercepts are (2, 0) and (−2, 0), which f(2) = 0, f(−2) = 0,

therefore, the "numerator must exist (x + 2) and (x − 2) terms" --- (requirement 1).  

we can currently assume that f(x) = (x + 2)(x − 2).

p.s. f(x) = n(x)/d(x), n(x) is the numerator, and d(x) is denominator.

example

6-2

from the y-intercepts (0, 4)

"f(0) = 4 must be satisfy" --- (requirement 2), 

however, base on our pervious assumption,   f(0) = (0+2)(0−2) = −4,  which is missing a minus sign (−).

now, we currently assume that f(x) = −(x + 2)(x − 2).

6-3

base on the VA (vertical asymptotes), there are two poles at x=1, and x = −1.

poles goes to the denominator of a rational function, (due to the zero on the denominator)

therefore, the "denominator must exist (x+1) and (x −1) terms" --- (requirement 3) .

again, we can now assume the possible function is...

f(x) = −(x + 2)(x − 2)

           (x + 1)(x − 1)

example:

6-4

base on the HA (horizontal asymptotes), which is y = 1,

   lim         f(x)  =  constant (asymptotes)

  x->∞

Usually, the horizontal asymptotes exist only when the highest degree of numerator < the highest degree of denominator.

since we have a horizontal asymptotes at y = 1, so "  lim    f(x) =    lim     f(x) = 1 must be satisfy" --- (requirement 4) 

　                                                             ^{x->∞                  x->−∞}                                                  

therefore, 

1 ?= lim f(x)   = lim     −(x + 2)(x − 2)

        ^{x->∞          x->∞}    (x + 1)(x − 1)

                    = lim         −x^2 + 4   1/x^2

                       ^x->∞         x^2 −1     1/x^2

                     = lim        − 1 + 4/x^2

                        ^x->∞         1 −1/x^2

                    =    − 1 + 0

                             1 − 0

                    = −1

Therefore, we missing a minus sign in the f(x), therefore, add a minus sign on our assumption from 6-3, 

f(x) = −  −(x + 2)(x − 2)  =  (x + 2)(x − 2) 

               (x + 1)(x − 1)        (x + 1)(x − 1)

6-5

The last step, we shall re-check all four requirements.  They MUST all be satisfy. 

base on our assumption from 6-4, double check the following... 

"numerator must exist (x + 2) and (x − 2) terms" --- (requirement 1)     ... Satisfy

"f(0) = 4 must be satisfy" --- (requirement 2)                                      ... Satisfy

"denominator must exist ( x+1) and ( x −1) terms" --- (requirement 3)    ... Satisfy

"  lim    f(x) =    lim     f(x) = 1 must be satisfy" --- (requirement 4)        ... Satisfy

   ^{x->∞                  x->−∞}                                                    

Therefore, our assumption on 6-4 is correct. 

f(x) = (x + 2)(x − 2)

          (x + 1)(x − 1)

     =  x^2 − 4

         x^2 − 1

6-6 Check 

We can check our answer with any online function graphing tool or MATLAB,

type (x^2 - 4)/(x^2 - 1) into the tool, we get the exact same result as question (shown on Figure#2).

                                                                   Figure #2 

p.s.

Online Graphing  

http://www.walterzorn.com/grapher/grapher_e.htm

MATLAB

http://www.mathworks.com/

Question 2: Find domain, x-intercept points, y-intercept points, symmetry, all the asymptotes 

and find the actual function base on the given graph (shown on Figure#3).

                                           Figure#3

1 - Domain 

Base on Figure#3, we can easily see is continuous for all the value of x from −∞ to ∞,

therefore,  Domain (−∞, ∞)

2 - X- intercepts points

Base on Figure#3, the x-int points are (0,0), (2, 0) and (−2, 0) 

3 - Y- intercepts points

Base on Figure#3, the y-int point is (0, 0)

4 - Symmetric

There is symmetric about the y-axis, this is an even function, y(x) = y(−x).

5 - Asymptotes

No vertical asymptotes.

No horizontal asymptotes.

No slant asymptotes (oblique asymptotes).

6 - Actual Function

6-1

Let y = f(x)

From the information on x-intercepts points, 

1st, we can see that the function bounce back at (0, 0), it is a "double roots", therefore, x² must be a term of f(x).

2nd, we can see that the function pass through at (2, 0) and (−2, 0), they are "single root", therefore, (x + 2) and (x−2), must be a term of f(x).

So, f(x) = kx²(x + 2)(x−2), "k" is a unknown number that we need to find out.

6-2

The information of y-intercept (0, 0) is useless, because it is the same point as one of the x-intercepts point.

we can do nothing here, just move on.

6-3

There are one max point (0, 0) and two min points (?,−2) and (?, −2), but we are missing the exact value of x, 

at these three points, f '(x) = 0 due to the tangent slope equal zero.

This is a very useful information, which can allowed us to find useful point on the function, and lead us to find the value of "k".

f '(x) = d/dx kx²(x + 2)(x−2)

        = k d/dx x²(x² −4)

        = k d/dx (x⁴ −4x²)

        = k (4x³ −8x)

set f '(x) = 0

0 = k (4x³ −8x)

0 = 4x (x² −2)

x = 0, √2, −√2    therefore, the three points are --> (0, 0) (−√2, −2) and (√2, −2)

(0, 0) is a useless point, since it the same point as x-int and y-int, 

however, we can use (−√2, −2) and (√2, −2) to find "k",

by sub the point (√2, −2) into our function from 6-1, f(x) = kx²(x + 2)(x−2)

f(√2) = k(√2)²(√2 + 2)(√2−2)

          = k (2)(2 − 4)

          = −4k

which f(√2) = −2

so       −2 = −4k

             k = 1/2

Our final answer will be f(x) = (1/2) x²(x + 2)(x−2)

Answer: f(x) = (1/2) x²(x + 2)(x−2)

6-4 Check

Type (1/2)*(x^2)*(x+2)*(x-2) into online graphing tool or MATLAB, 

we can see it is exact the same as our question (shown on Figure #4)

                                                                   Figure #4 

Written by Kevin Tang (Apr 2, 2010)

[back]

Copyright 2010 - KEVKEVWORLD.NET